Subtraction of Whole Numbers
Subtraction of numbers with more than five digits can be done in the same way as we have learnt to do subtraction of smaller number earlier. We arrange the numbers one below the other in place-value columns. We start subtracting them one by one from the right most column and borrow if required, from the column on left.
Subtraction of whole numbers is discussed in the following two steps to subtract one large number from another large number:
We arrange the given numbers in columns, ones under ones, tens under tens, hundred under hundreds and so on. Step II:
Beginning with the ones, we go on subtracting column wise, borrowing if necessary, from the next column to the left.
We borrow from millions column to hundred thousands column from hundred thousands column to ten thousands column from ten thousands column to thousands column from thousands column to hundreds column from hundreds column to tens column and from tens column to ones column.
For Example:
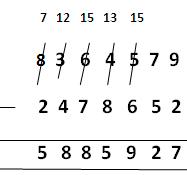
1. Subtract 2478652 from 8364579. Solution: We arrange the given numbers in columns (minuend on the top and subtrahend under it) and subtract as under:
8364579
- 2478652
We need to subtract the ones column and the tens column as usual because here we don’t need to borrow numbers as the bottom numbers are smaller than the numbers on the top.
Now we borrow 1 million from 8 millions. Then we get (8 - 1) = 7 millions in the millions column.
Now in place of 3 hundred thousands we have 13 hundred thousands in the hundred thousands column. Now borrow 1 hundred thousand from 13 hundred thousands. Then we get (13 - 1) = 12 hundred thousands in the hundred thousands column.
Then in place of 6 ten thousands we have 16 ten thousands in the ten thousands column. Now borrow 1 ten thousand from 16 ten thousands. Then we get (16 - 1) = 15 ten thousands in the ten thousands column.
Again, in place of 4 thousands we have 14 thousands in the thousands column. Now borrow 1 thousand from 14 thousands. Then we get (14 - 1) = 13 thousands in the thousands column.
5 hundreds + 1 thousand borrowed become 15 hundreds in the hundreds column.
Therefore, now we just need to subtract after borrowing the numbers since we observe that the bottom numbers are smaller than the numbers on the top.
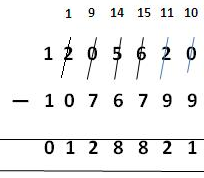
2. Subtract 1076799 from 1205620.
We arrange the given numbers in columns (minuend on the top and subtrahend under it) and subtract as under:
1205620
- 1076799
In this subtraction problem we observe that upto ten thousands column all the bottom numbers are bigger than the numbers on the top.
So, we will start borrowing numbers from hundred thousands column.
Now we borrow 1 hundred thousand from 2 hundred thousands. Then we get (2 - 1) = 1 hundred thousand in the hundred thousands column.
Now in place of 0 ten thousand we have 10 ten thousands in the ten thousands column. Now borrow 1 ten thousand from 10 ten thousands. Then we get (10 - 1) = 9 ten thousands in the ten thousands column.
Then in place of 5 thousands we have 15 thousands in the thousands column. Now borrow 1 thousand from 15 thousands. Then we get (15 - 1) = 14 thousands in the thousands column.
Again, in place of 6 hundreds we have 16 hundreds in the hundreds column. Now borrow 1 hundred from 16 hundreds. Then we get (16 - 1) = 15 hundreds in the hundreds column.
Now in place of 2 tens we have 12 tens in the tens column. Now borrow one ten from 12 tens. Then we get (12 - 1) = 11 tens in the tens column.
0 ones + 1 ten borrowed become 10 ones in the ones column.
Therefore, now we just need to subtract after borrowing the numbers since we observe that the bottom numbers are smaller than the numbers on the top.
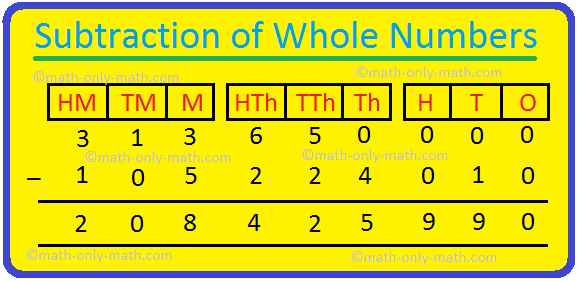
3. Subtract 3214658 from 5645789
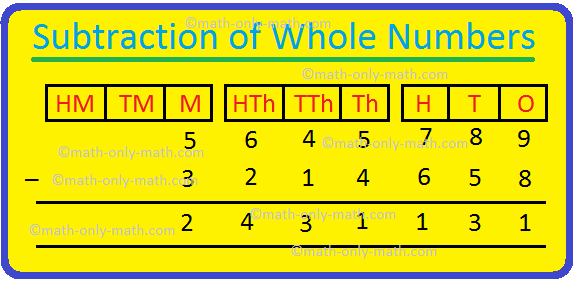
Hence, 5645789 – 3214658 = 2431131.
2. Subtract 65248907 from 86165281
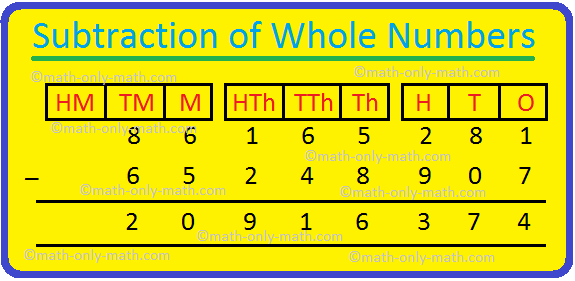
Hence, 86165281 – 65248907 = 20916374
Word Problems on Subtraction of Whole Numbers:
A factory produced 313650000 candies in the month of December for Christmas. Out of these 105224010 were of lavender flavor. How many of the candies were not of lavender flavor?
Number of candies produced = 313650000
Number of candies of lavender flavor = 105224010
Number of candies not having lavender flavor
Hence, the total number of candies not having lavender flavor = 208425990.
Solve the given Word Problems on Subtraction of Whole Numbers:
1. A country has a population of 651399888. If 304628040 are females, then how many are males?
Answer: 346771848
2. 1432884 people visited the international book fair on Saturday and Sunday. The number of people visiting the fair on weekdays was 89745 less than that on weekend. How many people visited the fair on weekdays?
Answer: 1343139
3. Find the number that is:
(i) 30000 less than 183645800
(ii) 1200000 less than 483625900
(i) 183615800
(ii) 482425900
Note: We can subtract 7-digit, 8-digit and 9-digit numbers in the same way as we subtract 5-digit and 6-digit numbers.
We know, the number which is to be subtracted is known as 'subtrahend' and the number from which it is subtracted is known 'minuend' and the answer we get is known as the 'difference' the number is placed below the number from which it is subtracted.
● Operations On Whole Numbers
- Addition Of Whole Numbers.
- Word Problems on Addition and Subtraction of Whole Numbers
- Subtraction Of Whole Numbers.
- Multiplication Of Whole Numbers.
- Properties Of Multiplication.
- Division Of Whole Numbers.
- Properties Of Division.
- Word Problems on Multiplication and Division of Whole Numbers
- Worksheet on Addition and Subtraction of Large Numbers
- Worksheet on Multiplication and Division of Large Numbers
- Worksheet on Operations On Whole Numbers
5th Grade Math Problems From Subtraction of Whole Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy

Recent Articles
2nd grade math Worksheets | Free Math Worksheets | By Grade and Topic
Nov 20, 24 01:00 PM

2nd Grade Measurement Worksheet | Measuring Length, Mass and Volume
Nov 20, 24 12:50 AM
2nd Grade Fractions Worksheet | Basic Concept of Fractions | Answers
Nov 20, 24 12:16 AM

2nd Grade Math Practice | Second Grade Math |2nd Grade Math Worksheets
Nov 18, 24 02:23 PM
Worksheet on Addition of Length | Word Problems on Addition of Length
Nov 17, 24 10:29 PM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Child Login
- Kindergarten
- Number charts
- Skip Counting
- Place Value
- Number Lines
- Subtraction
- Multiplication
- Word Problems
- Comparing Numbers
- Ordering Numbers
- Odd and Even
- Prime and Composite
- Roman Numerals
- Ordinal Numbers
- In and Out Boxes
- Number System Conversions
- More Number Sense Worksheets
- Size Comparison
- Measuring Length
- Metric Unit Conversion
- Customary Unit Conversion
- Temperature
- More Measurement Worksheets
- Writing Checks
- Profit and Loss
- Simple Interest
- Compound Interest
- Tally Marks
- Mean, Median, Mode, Range
- Mean Absolute Deviation
- Stem-and-leaf Plot
- Box-and-whisker Plot
- Permutation and Combination
- Probability
- Venn Diagram
- More Statistics Worksheets
- Shapes - 2D
- Shapes - 3D
- Lines, Rays and Line Segments
- Points, Lines and Planes
- Transformation
- Quadrilateral
- Ordered Pairs
- Midpoint Formula
- Distance Formula
- Parallel, Perpendicular and Intersecting Lines
- Scale Factor
- Surface Area
- Pythagorean Theorem
- More Geometry Worksheets
- Converting between Fractions and Decimals
- Significant Figures
- Convert between Fractions, Decimals, and Percents
- Proportions
- Direct and Inverse Variation
- Order of Operations
- Squaring Numbers
- Square Roots
- Scientific Notations
- Speed, Distance, and Time
- Absolute Value
- More Pre-Algebra Worksheets
- Translating Algebraic Phrases
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
- Algebraic Identities
- Quadratic Equations
- Systems of Equations
- Polynomials
- Inequalities
- Sequence and Series
- Complex Numbers
- More Algebra Worksheets
- Trigonometry
- Math Workbooks
- English Language Arts
- Summer Review Packets
- Social Studies
- Holidays and Events
- Worksheets >
- Number Sense >
- Subtraction >
Subtraction Word Problem Worksheets
The extensive set of subtraction word problems featured here will require the learner to find the difference between minuends and subtrahends, which includes problems with regrouping and without regrouping. This large collection of printable word problem worksheets, ideal for children in kindergarten through grade 4 features scenarios that involve single-digit subtraction, two-digit subtraction, three-digit subtraction, and subtraction of large numbers up to six digits. Give yourself a head-start with our free subtraction worksheets!

Word Problems for Beginners: 0 to 10
Find the difference between the numbers that ranges from 0 to 10 in the set of kindergarten worksheets featured here. Use the answer key to verify your responses.
- Download the set

Subtraction within 20
Ascend from a beginner to a proficient in performing subtraction up to 20 as you explore this bunch of well-researched word problems and work out the difference within 20.

Two-digit Subtraction: No Regrouping (No Borrowing)
The series of worksheets for grade 1 and grade 2 presented here involve two-digit subtraction word problems that do not require regrouping. Find the differences between the two-digit subtrahends and minuends featured here.

Two-digit Subtraction: Regrouping (Borrowing)
The two-digit subtraction word problems presented in the 2nd grade worksheets here require regrouping (borrowing). Determine the difference between the two-digit numbers by following the place value columns correctly.

Theme based Subtraction Problems
The colorful theme-based worksheet pdfs for kids in 1st grade through 3rd grade are based on three engaging real-life themes - Beach, Italian Ice and Birthday Party.

Three-digit and Two-digit Subtraction
The set of subtraction word problem pdfs featured here will require grade 3 student to find the difference between three-digit minuends and two-digit subtrahends. Use the answer keys to verify your responses.

Three-digit Subtraction Word Problems
Each printable worksheet contains five word problems finding difference between three-digit numbers. Some problems may require regrouping.

Four-digit Subtraction Word Problems
This section contains subtraction word problems on finding the difference between four-digit numbers. Both borrowing and no borrowing problems are included. Some problems may involve subtraction across zero.

Advanced: Large Number Subtraction
The word problems featured in the 4th grade pdf worksheets here include large numbers with minuends and subtrahends up to six digits. Determine the difference between the large numbers by following the place value columns correctly.
Related Worksheets
» Addition Word Problems
» Subtraction within 10
» 2-Digit Subtraction
» Word Problems
Become a Member
Membership Information
Printing Help
How to Use Online Worksheets
How to Use Printable Worksheets
Privacy Policy
Terms of Use
Copyright © 2024 - Math Worksheets 4 Kids
This is a members-only feature!

Subtraction Word Problems (1-step word problems)
These lessons look at some examples of subtraction word problems that can be solved in one step, illustrating the use of bar models or block diagrams in the solution process.
Related Pages 2-step Subtraction Word Problems Using Bar Models Solving Word Problems Using Bar Models Singapore Math More Word Problems
We will illustrate how block diagrams can be used to help you to visualize the subtraction word problems in terms of the information given and the data that needs to be found. The block diagrams or block modeling method is used in Singapore Math.
Example: Jessica has 1135 beads. 604 beads are red and the rest are blue. How many blue beads does she have?
1135 – 604 = 531
She has 531 blue beads.
Example: James and Ken donated $2300 to a charitable organization. Ken donated $658. How much did James donate?
2300 – 658 = 1642 James donated $1642.
Example: The price of a car is $2795 and the price of a motorbike is $1063. What is the difference between the prices of the 2 vehicles?
Solution: 2795 – 1063 = 1732
The difference between the prices of the 2 vehicles is $1732.
Example: There are 967 chairs in a hall. During an event, 761 chairs were occupied. How many chairs were not occupied?
967 – 761 = 206 206 chairs were not occupied.
Examples of subtraction word problems
134 girls and 119 boys took part in an art competition. How many more girls than boys were there?
Mei Lin saved $184. She saved $63 more than Betty. How much did Betty saved?
John read 32 pages in the morning. He read 14 pages less in the afternoon. a) How many pages did he read in the afternoon? b) How many pages did they read altogether?
A visual way to solve world problems using bar modeling This type of word problem uses the part-whole model.
Example: Mr. Oliver bought 88 pencils. he sold 26 of them. How many pencils did he have left?
A visual way to solve world problems using bar modeling This type of word problem uses the part-whole model. Because the part is missing, this is a subtraction problem.
Example: There are 98 hats, 20 of them are pink and the rest are yellow. How many yellow hats are there?
Example: Cayla did 88 sit-ups in the morning. Nekira did 32 sit-ups at night. How many more sit-ups did Cayla do than Nekira?
How to use bar modeling in Singapore math to solve word problems that deal with comparing?
Example: Adam has 11 fewer lollipops than Hope. If Adam has 16 lollipops, how many lollipop does Hope have?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

- $ 0.00 0 items
Subtract Whole Numbers
1.3 subtract whole numbers.
The topics covered in this section are:
- Use subtraction notation
- Model subtraction of whole numbers
- Subtract whole numbers
- Translate word phrases to math notation
- Subtract whole numbers in applications
1.3.1 Use Subtraction Notation
Suppose there are seven bananas in a bowl. Elana uses three of them to make a smoothie. How many bananas are left in the bowl? To answer the question, we subtract three from seven. When we subtract, we take one number away from another to find the difference . The notation we use to subtract $3$ from $7$ is
We read $7-3$ as seven minus three and the result is the difference of seven and three .

Subtraction Notation
To describe subtraction, we can use symbols and words.
Translate from math notation to words:
- We read this as eight minus one . The result is the difference of eight and one .
- We read this as twenty-six minus fourteen . The result is the difference of twenty-six and fourteen .
1.3.2 Model Subtraction of Whole Numbers
A model can help us visualize the process of subtraction much as it did with addition. Again, we will use base-$10$ blocks. Remember a block represents $1$ and a rod represents $10$. Let’s start by modeling the subtraction expression we just considered, $7-3$.
MANIPULATIVE MATHEMATICS
Doing the Manipulative Mathematics activity Model Subtraction of Whole Numbers will help you develop a better understanding of subtracting whole numbers.
Model the subtraction: $8-2$.
Model the subtraction: $13-8$.
As we did with addition, we can describe the models as ones blocks and tens rods, or we can simply say ones and tens.
Model the subtraction: $43-26$.
Because $43-26$ means $43$ take away $26$, we begin by modeling the $43$.

Now, we need to take away $26$, which is $2$ tens and $6$ ones. We cannot take away $6$ ones from $3$ ones. So, we exchange $1$ ten for $10$ ones.

Now we can take away $2$ tens and $6$ ones.

Count the number of blocks remaining. There is $1$ ten and $7$ ones, which is $17$.
1.3.3 Subtract Whole Numbers
Addition and subtraction are inverse operations. Addition undoes subtraction, and subtraction undoes addition. We know $7-3=4$ and $4+3=7$. Knowing all the addition number facts will help with subtraction. Then we can check subtraction by adding. In the examples above, our subtractions can be checked by addition.
Subtract then check by adding:
To subtract numbers with more than one digit, it is usually easier to write the numbers vertically in columns just as we did for addition. Align the digits by place value, and then subtract each column starting with the ones and then working to the left.
Subtract then check by adding: $89-61$.
Our answer is correct.
When we modeled subtracting $26$ from $43$, we exchanged $1$ ten for $10$ ones. When we do this without the model, we say we borrow $1$ from the tens place and add $10$ to the ones place.
How to: Find the Difference of Whole Numbers
- Write the numbers so each place value lines up vertically.
- Subtract the digits in each place value. Work from right to left starting with the ones place. If the digit on top is less than the digit below, borrow as needed.
- Continue subtracting each place value from right to left, borrowing if needed.
- Check by adding.
Subtract: $43-26$.
Subtract then check by adding: $207-64$.
Subtract then check by adding: $910-586$.
Subtract then check by adding: $2,162-479$.
1.3.4 Translate Word Phrases to Math Notation
As with addition, word phrases can tell us to operate on two numbers using subtraction. To translate from a word phrase to math notation, we look for key words that indicate subtraction. Some of the words that indicate subtraction are listed in Table 1.3 below.
Translate and then simplify:
- the difference of $13$ and $8$
- subtract $24$ from $43$
Part 1 The word difference tells us to subtract the two numbers. The numbers stay in the same order as in the phrase.
Part 2. The words subtract from tells us to take the second number away from the first. We must be careful to get the order correct.
1.3.5 Subtract Whole Numbers in Applications
To solve applications with subtraction, we will use the same plan that we used with addition. First, we need to determine what we are asked to find. Then we write a phrase that gives the information to find it. We translate the phrase into math notation and then simplify to get the answer. Finally, we write a sentence to answer the question, using the appropriate units.
The temperature in Chicago one morning was $73$ degrees Fahrenheit. A cold front arrived and by noon the temperature was $27$ degrees Fahrenheit. What was the difference between the temperature in the morning and the temperature at noon?
We are asked to find the difference between the morning temperature and the noon temperature.
A washing machine is on sale for $\$399$. Its regular price is $\$588$. What is the difference between the regular price and the sale price?
We are asked to find the difference between the regular price and the sale price.
CC Licensed Content, Original
- Revision and Adaptation. Provided by: Minute Math. License: CC BY 4.0
CC Licensed Content, Shared Previously
- Marecek, L., Anthony-Smith, M., & Mathis, A. H. (2020). Introduction to Whole Numbers. In Prealgebra 2e. OpenStax https://openstax.org/books/prealgebra-2e/pages/1-3-subtract-whole-numbers . License: CC BY 4.0 . Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction .
Share this:
- No products in the cart.


Subtraction Practice Questions
Click here for questions, click here for answers.
GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy
Terms and Conditions
Corbettmaths © 2012 – 2024

IMAGES
VIDEO
COMMENTS
Let us solve some word problem examples. Word problems on adding and subtracting of large numbers: 1. The population of a country in 1990 was 906450600 and next year it is increased by 9889700. What was the population of that country in the year of 1991? The population of a country in 1990 = 906450600.
The Process of Subtracting Whole Numbers. To subtract two whole numbers, The process. Write the numbers vertically, placing corresponding positions in the same column. 48 − 35 _. Subtract the digits in each column. Start at the right, in the ones position, and move to the left, placing the difference at the bottom. 48 − 35 _ 13.
These lessons look at simple examples of subtraction word problems. Words like ‘difference’, ‘less’, ‘take away’, ‘loss’ usually means that subtraction is involved. For subtraction, take note which number has to be subtracted from which number. Subtracting in the wrong order will give you the wrong answer. Andy has 53 marbles.
That will look like this: money left = 5000 - 2000 - 500 - 300. Step 2: Solve the equation. To solve the equation, all we need to do is perform the subtraction operations and find the difference ...
2. Subtract 1076799 from 1205620. Solution: We arrange the given numbers in columns (minuend on the top and subtrahend under it) and subtract as under: 1205620. - 1076799. In this subtraction problem we observe that upto ten thousands column all the bottom numbers are bigger than the numbers on the top.
The word problems featured in the 4th grade pdf worksheets here include large numbers with minuends and subtrahends up to six digits. Determine the difference between the large numbers by following the place value columns correctly. Download the set. Explore these subtraction word problem worksheets that deal with real-life situations.
A visual way to solve world problems using bar modeling This type of word problem uses the part-whole model. Because the part is missing, this is a subtraction problem. Example: There are 98 hats, 20 of them are pink and the rest are yellow. How many yellow hats are there? Show Video Lesson
1.3.2 Model Subtraction of Whole Numbers. A model can help us visualize the process of subtraction much as it did with addition. Again, we will use base- 10 blocks. Remember a block represents 1 and a rod represents 10. Let’s start by modeling the subtraction expression we just considered, 7 − 3. We start by modeling the first number, 7.
Subtract Whole Numbers. Addition and subtraction are inverse operations. Addition undoes subtraction, and subtraction undoes addition. We know \(7 − 3 = 4\) because \(4 + 3 = 7\). Knowing all the addition number facts will help with subtraction. Then we can check subtraction by adding. In the examples above, our subtractions can be checked by ...
The Corbettmaths Practice Questions on Subtraction. Welcome; Videos and Worksheets; Primary; 5-a-day. 5-a-day GCSE 9-1; 5-a-day Primary; 5-a-day Further Maths; More.